Measure the impedance of an AM-band antenna-ground system

Quick Summary: This Article describes a method to measure the series capacitive and resistive parameters of the impedance of an antenna-ground system vs frequency. Results from measurements on an attic antenna are given.

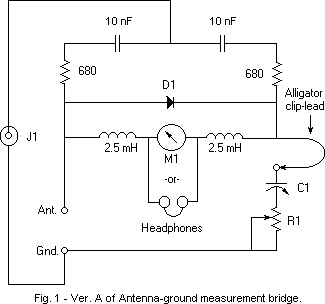
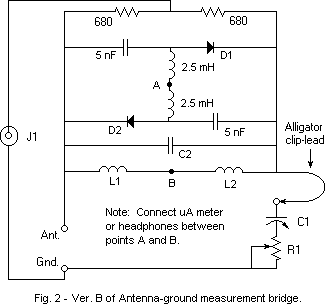
The circuit in Fig. 1 was inspired by an Article in The Crystal Set Society Newsletter of Jan 1, 1995. It was written by Edward Richley. He used a 1 MHz crystal oscillator for his source, so had no problem with using a 200 uA meter. I use a sine wave function generator for my RF source, but a radio Service man's oscillator may also be used if it has enough output. Either of these sources cannot supply as much signal as the xtal oscillator, so I had to increase sensitivity. That's what the 2.5 mH chokes and 5 nF caps are for. The 2.5 mH chokes eliminate RF loading by any resistive component of the meter or phones on the diode detector. The 5 nF caps eliminate resistive DC loading on the detector from the two 680 ohm resistors. I lay out the components breadboard style on a nonconductive table to minimize stray capacity, keep connections short, and especially keep the signal source lead of J1 away from the connections to each end of D1. In my setup D1 is a 1N34A, M1 is a 0-20 uA DC meter, R1 is a 75 ohm non-inductive carbon pot and C1 is a two gang variable cap of 365 pF per section. I parallel the two sections when the antenna capacitance is above 365 pF. A lower sensitivity meter can be used than the one used here, at the cost of a requiring a higher applied signal to J1.

If a sensitive enough meter is not available, a pair of high impedance phones (2000 ohms DC resistance) or preferably, a sound powered pair with the elements wired in series can be used. In this case, the generator must have its AM audio modulation turned on at its highest level. A modulation frequency of about 1 kHz is recommended. If the meter is used, do not connect the phones. If phones are used, do not connect a meter.

To use the bridge, tune the generator to a frequency of interest. Adjust C1 and R1 for minimum deflection on M1 or a null of the modulation tone in the phones. Increase the RF signal to J1 as much as possible in order to get the sharpest and most precise null. Measure the resistance of R1 with an ohmmeter. Use any desired method to measure C1. I use the cap. measurement range of my Fluke DVM. I'm sure the reader does not need to be reminded that this test involves radiating a weak RF signal from the antenna when making the measurements, so the length of time the generator is on should be kept as short as possible.

Possible issues: More sensitivity is needed or interference from antenna pickup of local stations obscures the bridge null.

If insufficient signal is available from the RF generator to provide satisfactory meter readings, one can use the more sensitive broadband circuit shown in Fig. 2. The values of L1 and L2 are 2.5 mH and C2 is set to zero in the broadband version. A full wave rectifier is used instead of the half wave one used in Fig.1 and it gives about twice the output. One can also change from using 1N34A diodes and try Schottky Zero Bias detector diodes such as the Agilent HSMS-2850 in either circuit. The HSMS-2855 Zero Bias diode is especially suitable for use in the circuit shown in Fig. 2 since it is a package having two independent diodes, one for D1 and the other for D2. One must be cautious when using the HSMS-2855 because the diodes can be damaged by the application of too strong a signal to J1. This can happen if the signal generator signal is very strong when the bridge is greatly unbalanced. It's best to start with a weak signal, balance the bridge, then increase the signal if necessary.

If the signal from the RF generator is not strong enough to override local pickup, thus obscuring the meter null, selectivity may be added to the bridge shown in Fig. 2 by making use of C2 and changing L1 and L2. If L1 and L2 are changed to, say, 10 uH inductors and C2 is made equal to 1200 pF, the bridge will be tuned to about 1 MHz. These changes will reduce the influence of local pickup upon measurement of antenna-ground impedance at 1 MHz. One suitable 10 uH inductor is Mouser's "Fastron" #434-23-100.

If one uses headphones instead of a meter as the null indicator, even greater sensitivity can be achieved by AF modulating the bridge signal generator and connecting a parallel L/C tuned to the modulating frequency of the generator across the phones. This will filter out much of the interfering cross talk from local pickup and pass the modulation tone with little loss. Suggested values are L=47 mH and C=0.5 uF if the modulating frequency used is about 1 kHz. A low cost coil having an inductance of 47 mH and a Q of about 9 at 1 kHz is available from Mouser as a Fastron Plugable Shielded coil, #434-02-473J ($1.20 each). Greater selectivity against cross-talk can be obtained by decreasing the inductance and increasing the capacitor.

I live about 9 miles from WOR and 12 from WABC, both 50 kW stations. 10 volts peak-to peak applied to the bridge overrides the local radio station pickup sufficiently to provide a clear null on the meter when using the circuit shown in Fig. 1 when using a 1N34A diode. A useable null with an applied signal of only 1.5 volts p-p can be obtained when using the circuit in Fig. 2 with zero bias detector diodes, sound-powered phones instead of a meter and the parallel LC filter.

If the RF source has too great a harmonic content, the bridge balance null will become less deep and sharp. That's why I used a sine wave function generator to assure a low harmonic content. If one uses a function generator for pure sine waves, make sure the symmetry control is set for best symmetry (minimum reading on the bridge microampmeter). In April 2004 Tom Polk published a description and schematic for a low distortion medium wave home brew signal generator. It looks very good, and can be found at: http://www.beecavewoods.com/testequipment/sinewave.html .
If the resistance of a specific antenna-ground system is greater than 100 ohms, use a pot of a higher value than 100 ohms.
A typical antenna-ground system will show a capacitance of a few hundred pF at the low end of the BC band. Because of the series inductance in the system, the measured capacitance will rise at higher frequencies. At a high enough frequency the system will go into series resonance and the bridge will not be able to be balanced. To measure the system series resistance at or above this resonance, place a hi Q capacitor of, say 100 to 220 pF in series with the antenna. That will raise the resonant frequency sufficiently so that the capacitor-antenna-ground circuit will be capacitive, a null can be obtained and the resistive component determined. An NPO ceramic or mica cap should be OK.
At my location, detected signals from local strong stations show up as fluctuations at about 15% of full scale on the meter, but are not strong enough to obscure the bridge nulls from of the signal generator's signal.
Unless the signal generator connected to J1 is battery powered (most aren't), it is important to put a common-mode radio frequency choke in the power line to the generator. I made mine by bundling a length of 18 ga. lamp cord into an 18 turn coil having a 9 inch diameter, and then fitting a male AC plug on one end and a female socket on the other. The turns were kept together using twist ties.

The main practical thing one can do with the bridge is to Measure and Monitor antenna-ground circuit resistance. This resistance comes primarily from the physical ground, not the antenna and ground connecting leads or radiation resistance of the antenna. Any increase in the antenna-ground resistance serves to reduce the signal power available from the antenna. Any decrease, of course increases it. A halving of the antenna-ground system resistance provides a 3 dB increase in available signal power, if one properly rematches to the crystal radio set input circuit.

Measure: One can experiment with different grounds and various ground paralleling schemes to come up with the one that has the lowest resistance. Use of this one will result in maximizing the available signal power (more volume). Experiments using a counterpoise ground can be made.
Monitor: As has been recently been posted on the Yahoo Club: thecrystalsetradioclub, earth ground resistance deteriorates (increases) over time. This results in a gradual decrease in available signal power (less volume). Periodic measurement can alert one if this is happening so steps can be taken to correct the problem.

The other thing one can do, if one is mathematically engineering a crystal radio set, is to use the R and C values as parameters in the design. See Article #22.

Measurement results on an indoor attic antenna system:
My present external (as opposed to loop) antenna is in the attic. The horizontal element used to be made up of 7 twisted strands of #26 copper wire (17 ga.), suspended by strings about 1 1/2 feet below the peak of an asphalt shingled roof. It runs along under the peak and parallel to it for 53 feet. The wire is about 24 feet above ground level. The lead-in, connected to the center of the horizontal wire, runs horizontally, at a right angles for about 9 feet and then drops down vertically to the crystal radio set location, about four feet above ground level. The ground system consists of a connection to the cold water supply in parallel with a connection to the hot water baseboard heating system. To achieve a low inductance ground connection I use 300 ohm TV twinlead, both conductors soldered in parallel, for each lead. The addition of a connection to the AC neutral does not seem to reduce the inductance or resistance of this antenna-ground system. I always suggest trying the addition of a connection to the AC neutral. Sometimes it helps.

The measured antenna-ground system capacitance was 295 pF at 0.5 MHz, 325 at 1.0 MHz, 410 at 1.5 MHz and and 660 at 2.0 MHz initially. The respective series resistances measured: 17, 12, 10 and 14 ohms. The equivalent reactance elements of this antenna are a capacitance of 285 pF in series with an inductance of 12.5 uH. Since my ground is composed of the house cold water supply pipes in parallel with the the hot water baseboard heating system pipes, much of the capacitance from the horizontal attic antenna wire is to them and the roof, not a real resistive earth ground. That, I think explains the low resistance and high capacitance readings. Probably the ground system is acting as a sort of counterpoise.

I decided to see if I could get greater signal pickup by changing to a very crude simulation of a flattop antenna. To do this, I paralleled the antenna wire with a piece of TV twinlead connected to it at each end and at the point of down-lead takeoff. The twinlead was separated from the 7/26 wire by about 2 1/2 feet. The new measured antenna-ground system parameters became: Capacitance: 430 pF at 0.5 MHz, 510 at 1.0 MHz and 860 at 1.5 MHz. The respective series resistance values became: 15, 12 and 11 ohms. The equivalent reactance elements became a capacitance of 405 pF in series with an inductance of 14.2 uH. Signal pickup increased by a negligible 0.8 dB at 710 kHz, and even that was, I'm sure, within experimental error.

One may want to compare these equivalent impedance components with the 'Standard Dummy Antenna', as specified in 1938 by the IRE (Institute of Radio Engineers) in 'Standards on Radio Receivers'. My reference for this is Terman's Radio Engineer's Handbook, first edition, 1943, pp 973 and 974. A rather complex equivalent circuit for the antenna is shown on page 974. It is stated that a simpler alternative network, given in footnote #2 on page 973, can be used when only the BC band is of interest. It consists of the series combination of a 200 pF capacitor, 25 ohm resistor and 20 uH inductor. Terman states that the two antenna equivalent circuits have closely the same impedance characteristics in the BC band. The impedance graph on page 974 and the impedance from the series combination of 200 pF, 25 ohm resistor and 20 uH differ, particularly in the resistive curve in the complex equivalent circuit. The 25 ohm resistance in the simplified circuit is probably taken from the resistance in the complex circuit, at the geometric center of the BC band. This resistance is shown as constant in the simplified circuit, and as a strong function of frequency in the more complex circuit. It is suggested that the complex equivalent circuit is theoretically derived, assuming a perfect ground and therefore does not include the resistance of the ground return path. The ground circuit can easily add 15-50 or more ohms to the circuit.

How to measure the impedance of an AM-band antenna-ground system, what one can do with the results, along with some measurements