Practical design considerations, helpful definitions of terms and useful explanations of some concepts used in this Site

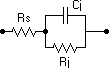
1.  An explanation as to why some diodes that work well in a broadcast band crystal set cause low sensitivity and selectivity when used at Short Waves:  The parasitic (approximately fixed) series resistance Rs of a diode is in series with the parallel active elements. The nonlinear active elements are the junction resistance Rj, which is a function of current through the diode, and the junction capacitance Cj, which is a function of the voltage across it.

The parasitic series resistance of some 1N34 diodes can be pretty high, and in series with the junction capacitance, make that capacitance have a rather low Q at high frequencies.  This capacitance is, in a crystal radio set, effectively in parallel with the RF tank. The tank usually has a small value tuning capacitor itself, so the overall tank circuit Q is reduced at high frequencies.  This is the main reason why diodes having large values for Rs and CJ perform poorly at high frequencies. 

2.  An explanation of the meaning and use of dB and dBm:  In the acronym dBm, "d" means one-tenth.  "B" refers to the Bel and is named after Alexander Graham Bell.  The Bel is used to express the ratio of two powers, say (Output Power)/(Input Power).  Let's call this power ratio "(pr)".  Mathematically, a power ratio, expressed in Bels, is equal to the logarithm of the ratio of the two powers.  B=log (pr).  If the two powers are equal, the power ratio expressed in Bels is 0 B.  This is because the log of one is zero.  Another illustration:  Assume that the power ratio is twenty. (Pr)=20.  The logarithm of 20 is about 1.3. This power ratio in Bels is 1.3 B.  One decibel is equal to 0.1 Bel.  That is, 10 dB=1 B.  If we express the two power ratios mentioned above (1 and 20) in dB, we get 0 dB and about 13 dB.

So far, we have seen that the decibel is used to express the ratio of two powers, it is not a measure of a power level itself.  A convenient way to express an actual power level using dB is to use a standard implied reference power for one of the powers.  dBW does this.  It expresses the ratio of a power to the reference power (One Watt in this case).  dBm uses a reference power of one milliwatt.  A power level of, say 100 milliwatts, can be said to be a power level of +20 dBm (twenty dB above one milliwatt).  Why?  (100 milliwatts)/(1 milliwatt)=100.  The logarithm of 100 is 2.  10 times 2 equals 20.

The convenient thing about using dB comes from a property of logarithms:  The logarithm of the product of two numbers is equal to the sum of the logarithm of each number, taken separately.  An illustration:  If one has a power source of, say 2.5 mW and amplifies it through an amplifier having a power gain of, say 80 times, the output power is 2.5 X 80=200 mW.  2.5 mW expressed in dBm is +4 about dBm.  A power gain of 80 times is about +19 dB.  The output power is 4+19=+23 dBm.

3.  Maximum Available Power:  If one has a voltage source Vs with an inaccessible internal resistance Rs, the load resistance to which the most power (Pa) can be delivered is equal to Rs.  Pa is called the 'maximum available power' from the  source Vs, Rs.  Any load resistance other than one equal to the source resistance, Rs, will absorb less power.  This applies whether the voltage is DC or AC (RMS).  The formula for power absorbed in a resistance is "voltage-squared divided by resistance".  In the impedance matched condition, because of the 2 to 1 voltage division between the source resistance and load resistance, one-half of the internal voltage Vs will be lost across the internal source resistance.  The other half will appear across the load resistance.  The actual power available to the load will be, as indicated in the preceding relation: Pa = [(Vs/2)^2]/Rs = (Vs^2)/(4*Rs).  Again, in the impedance matched condition, the total power delivered to the series combination of source and load resistance is divided up into two halves.  One half is unavoidably lost in the internal source resistance.  The other half is delivered as "useful output power" to the load resistance.

The 'maximum available power' approach is useful when measuring the insertion power-loss of two-port devices such as transformers, amplifiers and crystal radio sets, which may not exhibit an input or output impedance that is matched to the power source.  The input impedance may be, in fact a combination of resistive and reactive components.  If the Vs,Rs source is connected to a resistive load (Ro) of value equal to Rs ohms, it will receive and dissipate a power of Pa Watts.  This is the maximum available power from the Vs, Rs source, so we can say we have a 'no loss' situation.  Now, assume that a transformer or other two-port device is inserted between the Vs,Rs source and Ro, and that an output voltage Vo is developed across Ro.  The output power is (Vo^2)/Ro.  The 'insertion power loss' can now be calculated.  It is: 10*log (output power)/(maximum available input power) dB.  After substituting terms, the equation becomes:  Insertion power loss =10*log [(Vo/Vs)^2)*(4*Rs/Ro)] dB.

If the input voltage is referred to by its peak value (Vsp) as it is in a SPICE simulation, instead of by its RMS value, the equation changes.  The RMS voltage of a sine wave is equal to the peak value of that wave divided by the "square root of 2".  Since the power equation squares the voltage, the equation for the 'available input power' changes to Pa = (Vsp^2)/(8Rs).

4.  Diode Saturation Current and Ideality Factor:  Saturation current is abbreviated as Is in all of these articles.  Assume that one connects a DC voltage source to a diode with the polarity of the voltage source such as to bias the diode in the back direction.  Increase the voltage from zero.  If the diode obeys the classic Shockley ideal equation exactly, the current will start increasing, but the increase will flatten out to a value called the saturation current as the voltage is further increased.  That is, as the voltage is increased, the current will asymptotically approach the saturation current for that diode.  A real world diode has several mechanisms that cause the current to actually keep increasing somewhat and not flatten out as the back direction voltage is further increased.  Diode manufacturers characterize this as reverse breakdown and specify that the back current will be less than a specified value, say 10 uA at a specified voltage, say 30 V, called the reverse breakdown voltage.  BTW there are other causes of excessive reverse current that are collectively referred to as reverse bias excess leakage current.  Some diodes have a sharp, controlled increase in reverse current at a specified voltage.  These diodes are called Zener diodes.

Diode Saturation Current is a very important SPICE parameter that, along with the diode Ideality Factor n, determines the actual diode current when it is forward biased by at particular DC Voltage.  Id=Is*(e^(Vd/(0.026*n)-1) at room temperature.  This expression ignores the effect of the parasitic series resistance of the diode because it has little effect on the operation of crystal radio sets at the low currents usually encountered.  Here Id is the diode current, e is the base of the natural logarithms (2.7183...),  ^ means raise the preceding symbol to the power of the expression that follows (Sometimes e^ is written 'exp'), * means multiply the preceding and following symbols, VD is the voltage across the diode and n equals the "Ideality factor" of the diode.  At low signal levels, most detector diodes have an n of between 1.05 and 1.2).  The lower the value of n, the higher will be the weak signal sensitivity.  One can see that Is is a scaling factor for the actual curve generated by the factor (e^(VD/(0.026*n)-1).

Diode ideality factor (n):  The value of n affects the low signal-level sensitivity of a diode detector and its RF and audio resistance values.  n can vary between 1.0 and 2.0.  The higher the value of n, the worse the low signal level detector sensitivity.  The low signal level RF and audio resistances of a diode detector vary directly with the value of n.  Schottky diodes usually have a value of n between 1.03 and 1.10.  Good germanium diodes have an n of about 1.07 to 1.14 when detecting weak signals.  Silicon p-n junction diodes such as the 1N914 have values of n of about 1.8 at low currents and therefore have a lower potential sensitivity as diode detectors than Schottky and germanium point contact diodes.  The value of n in Schottky diodes seems to be approximately constant over the full range of currents and voltages encountered in crystal radio set operation, but varies with diode current in silicon p-n junction and germanium point contact diodes.  A way of thinking about n is to consider it as a factor that effectively reduces the applied signal voltage to a diode detector compared to the case of using an ideal diode having an n of 1.0.  Less applied signal, of course, results in less detected output.

Here are a few bits of information relative to diodes:

Typically, if a diode is biased at 0.0282*n volts in the forward direction, it will pass a current of 2 times its Is.  If it is biased at 0.0182*n volts in the reverse direction, it will pass a current of 0.5 times its Is.  If a diode is biased at 0.0616*n volts in the forward direction, it will pass a current of 10 times its Is.  If it is biased at -0.0592*n volts, it will pass a current of -0.9 times its Is. These values are predicted from the classic Shockley equation.  In the real world, reverse current can depart substantially from values predicted by the equation because of effects not modeled (the reverse current becomes higher).  Gold bonded germanium diodes usually depart somewhat from the predicted values when operated in the forward direction.  The effect appears as an increase of Is when measurements are made at currents above about 6 times the low-current Is.

Values of Is and n determine the location of the apparent 'knee" on a linear graph of the diode forward current vs. forward voltage. See Article #7.  An easy way to estimate the approximate value of Is can be found in Article #4, section 2.  A method of measuring Is and n is given in Article #16.

If one connects two identical diodes in parallel, the combo will behave as a single diode having twice the Is, and the same n as one of them.  If one connects two identical diodes in series, the combo will behave as a single diode having twice the n and the same Is as one of them.  This connection results in a diode having 3 dB less potential weak signal output than one of the diodes by itself.

5.  Explanation of why, in a diode detector, and by how much, the RF input resistance and audio output resistances change as a function of input signal power.  Refer to the second schematic in Article #1. The output load will be considered to be a resistor connected across the "Audio Output" terminals; call it Rl. No audio transformer is involved in the first part of this discussion.  Consider first, a diode detector that is well impedance-matched both at its input and its output when driven by a very low power RF input signal.   There will exist an appreciable power loss in the detector.  The input and output resistances of the diode detector will approximately equal each other and approach Rd (diode axis-crossing resistance)= 0.026*n/Is.  See part 3 above for a definition of terms.  For this illustration, let the diode have an Is of 38 nA and an n of 1.02.  Rd will be 700k Ohms.  This well impedance-matched condition will hold if the input power is raised from a low value, but only up to a point.  After that , the match will start to deteriorate.  At an input power about 15 dB above that of the square-law-linear crossover point, the match will have deteriorated to a VSWR of about 1.5:1  (VSWR = Voltage Standing Wave Ratio.).  A further increase of input signal power will result in a further increase of VSWR.  This means that the input and output resistances of the detector have changed from their previously well matched values.  The input resistance of the diode detector decreased from the value obtained in the well matched low power situation.  The output resistance increased.  The reason for this change is that a new law now governs input and output resistance when a diode detector is operated at a high enough power level to result in a low detector insertion power loss.  It now operates as a peak detector.  The rule here is that the CW RF input resistance of a diode peak-detector approaches ½ the value of its output load resistance.  Also, the audio output resistance approaches 2 times the value of the input AC source resistance.  Further, since the detector is now a peak detector, the DC output voltage approaches the "square root of 2" times larger than of the applied input RF RMS voltage. (It's equal to the peak value of that voltage).  These existence of these relationships is necessary so that in an ideal peak detector, the output power will equal the input power (No free lunch).  Summary: Output DC voltage equals sqrt2 times input RMS voltage.  Since the output power must equal the input power, and power equals voltage squared divided by resistance, the output load resistance must equal two times the source resistance, assuming impedance matched conditions prevail.  If we were to adjust the input RF source resistance to, say 495k ohms (reduce it by sqrt2) and the output load resistance to 990k ohms (increase it by sqrt2) by changing the input and output impedance transformation ratios, the insertion loss would become even lower than before the change and the input and output impedance matches would be very much improved (remember we are now dealing with high signal levels).  Note: It is assumed here that the peak reverse voltage applied to the diode when the signal is strong does not approach its peak reverse breakdown voltage rating.

A good compromise impedance match, from one point of view, occurs if one sets the RF source resistance to 0.794*Rd and the audio load resistance to 1.26*Rd (Rd=axis-crossing resistance of the diode).  With this setup, theoretically, the impedance match at both input and output remains very good over the range of signals from barely readable to strong enough to produce close to peak detection.  A measure of impedance match is "Voltage Reflection Coefficient", and in this case it is always better than 18 dB (VSWR better than 1.3).  Excess insertion loss is less than 1/3 dB and selectivity is largely independent of the signal level.  This situation can be attained in a real-world crystal set using an audio transformer if one connects a parallel RC (a "benny") in series with the transformer primary.  The resistor plus the DC resistance of the transformer primary is adjusted to equal the average AC resistance looking into the transformer primary. This combination approximates the effect of a straight resistive load, as used in the discussion above.  To determine the average AC input resistance of the audio transformer (when loaded by phones), multiply its step-up impedance ratio by the average AC impedance of the phones.  See Article #2 for a method of determining the average AC resistance of phones.

In the practical case of a real-world crystal set not using a "benny", the load the diode sees has a DC resistance component lower than its AC impedance. This unbalanced condition is worse when a transformer is used, as compared with phones only.  In this case, when going from reception of a weak to a strong signal, bad things start happening to selectivity:  As the RF signal strength starts increasing, the rectified DC current in the diode starts increasing faster than it does in the condition using a "benny". This causes the diode input and output resistances to fall. The result is a loaded down tank having reduced selectivity.  The use a "benny" prevents this, among other things from happening.

Information presented in Article #28 shows that, if the diode load resistance is made equal to Rd and the RF source resistance is made equal to Rd/2, the weak signal output of the detector will be about 2 dB greater than if both ports are impedance-matched!  There is little benefit when strong signals are received, since both input and output ports become impedance matched.

Here is an interesting conceptual view of a high signal level diode detector circuit:  Assume that it is driven with a sufficiently high level sine wave voltage so it operates in its peak detection mode, and is loaded with a parallel RC of a sufficiently long time const ant.  This detector may be thought of as a low loss impedance transformer with a two-to-one impedance step up from input to output, BUT having an AC input and a DC output, instead of the usual AC input and output.   The DC output power will approximately equal the AC input power and the DC output voltage will be about sqrt 2 times the RMS AC input voltage.

5A.  A comparison of conventional half-wave and half-wave voltage-doubling detectors:  Here is some info that may be of interest regarding conventional half-wave detectors vs. voltage doubling half-wave detectors when each is terminated with an output load of Ro. For illustration purposes we will assume the input voltage to the detector to be 1.0 volt RMS. The RF input resistance of the detector will be designated as Ri. All diodes have the same Is and n. It is assumed that good diodes such as a 5082-2835 Schottky, ITT FO-215 germanium or other are used. The info relates to the RF input resistance of detectors (it has a large effect upon selectivity) and their output audio resistance. See Point 4 in this Article for info on diode Is and n.

A high input power level is defined as one that is high compared to that at the LSLCP of the detector. A low input power level is defined as on that is low compared to that at the LSLCP of the detector. See "Quick Summary" in Article #15 for info on LSLCP.

1) Conventional half-wave detector operating at a high input signal power level: The detector, in this case, operates as a peak detector. Since it is a passive device, its output power will approximately equal its input power, under impedance-matched conditions. The output DC voltage will approach sqrt2 times the input RMS voltage, since the peak value of a sine wave is sqrt2 times its RMS value. For the input power, (1.0^2)/Ri, to equal the output power, [(1.0*sqrt2)^2]/Ro, the input RF resistance (Ri) must equal 1/2 Ro. That is, Ri=Ro/2. This illustrates the direct interaction between the RF input resistance and output audio resistive load. At high input power levels selectivity drops when the resistive audio output load value is lowered.  The audio output resistance of the detector approaches 2 times the RF source resistance driving it. If the diode were an ideal diode, the word "approximately" should be eliminated, and "approaches" should be changed to "becomes" .

2) Conventional half-wave detector operating at a low input signal power level: The detector, in this case, does not operate as a peak detector, and exhibits significant power loss. At low input signal power levels Ri approaches 0.026*n/Is ohms (diode axis-crossing resistance) and becomes independent of the value of Ro.

The audio output resistance of the detector approaches the same value as the axis-crossing resistance (see above).

3) Half-wave voltage doubling detector operating at a high input signal power level: The detector, in this case, operates as a peak detector. Since it is a passive device, its output power will approximately equal its input power, under impedance-matched conditions. The output DC voltage will approach 2.0*sqrt2 times the input RMS voltage, since the peak of a 1.0 volt RMS sine wave is sqrt2 times its RMS value. For the input power (1.0^2)/Ri to equal the output power [(1.0*2*sqrt2)^2]/Ro, the input RF resistance (Ri) must equal 1/8 Ro. That is, Ri=Ro/8. This illustrates the direct interaction between the RF input resistance and output audio resistive load. At high input power levels selectivity drops substantially if the output resistive audio load value is lowered.

The audio output resistance of the detector approaches 8 times the RF source resistance driving it. This fact is seldom recognized and it may be the cause of some of the problems encountered by those experimenting with doublers.

4) Half-wave voltage-doubler operating at a low input signal power level: The detector, in this case, does not operate as a peak detector, and it has significant power loss. At low input signal power levels Ri approaches (0.026*n/Is)/2 ohms and becomes independent of the value of Ro.

The audio output resistance of the detector approaches twice the axis-crossing resistance of the diode.

5) Summary:  At high input power levels, and with both input and output matched, power loss in both half wave and half wave voltage doubling detectors approaches zero dB.  Sound volume should be the same with either detector.  At low input power levels both detectors exhibit substantial power loss.  I believe, but have not proven, that at low input power levels the doubler has a higher power loss than the straight half wave detector, and should deliver less volume.

6.  Some misconceptions regarding Impedance matching and Crystal Radio Sets:  To understand the importance of impedance matching, one must first accept the concept of power.  A radio station accepts power from the mains and converts some of it to RF power which is radiated into space.  This power leaves the transmitting antenna at the speed of light and spreads out as it goes away from the antenna.  One can prove that power is radiated by substituting a LED diode for the regular diode, getting physically close enough to the station and then tuning it in.  The LED will light up (give off light power), showing that some power is being broadcast and that it can be picked up. Now back at home, if one tunes in the station one gets sound in the headphones.  What activates one's hearing system is the power of the perceived sound.  BTW, if one gets too much sound power in the ear for a long enough time, the power can be strong enough to break off some of the hair cells in the inner ear and reduce one's hearing sensitivity forever.  The theoretical best one can do with a crystal radio set setup is the following:  (1) Use an antenna-ground system to pick up as much as possible of the RF power passing through the air in its vicinity .  In general, a higher antenna will pick up more power from the passing RF waves than will a lower one.  (2) Convert the intelligence carrying AM sideband RF power into audio electrical power.  (3) Convert the electrical audio power into sound power and get that power  into the ear.

There are power losses at each of the three steps and our job is to minimize them in order to get as much of the sideband RF power passing through the vicinity of the antenna (capture area)  changed into audio power for our ears.  We want all of the "available power" at the antenna-ground system to be absorbed into the crystal radio set then  passed on through it to our headphones as sound.  However, some of it will be unavoidably lost in the RF tuned circuit.  If the input impedance of the crystal radio set is not correctly matched to the impedance of the antenna, some of the RF power hitting the input to the crystal radio set will be reflected back to the antenna-ground system and be lost.

An impedance-matched condition occurs when the resistance component of the input impedance of the crystal radio set equals the source resistance component of the impedance of the antenna-ground system.  Also, the reactive (inductive or capacitive) component of the impedance of the antenna-ground system must see an opposite reactive (capacitive or inductive) impedance in order to be canceled out.  In the impedance-matched condition, all of the maximum available power (See section on "Maximum Available Power" above) intercepted by the antenna-ground system is made available for use in the crystal radio set and none is reflected back towards the antenna to be lost.

Now we are at the point where confusion often exists:  The voltage concept vs. the power concept.  Let's assume that the diode detector has a RF input resistance of 90,000 Ohms.  Assume that the antenna-loaded resonant resistance of the tuned circuit driving it is 10,000 Ohms.  If one uses voltage concepts only, one might think that this represents a low loss condition.  NOT SO!  After all,  9/10 of the actual source voltage is actually applied to the detector.  If one impedance matches the 10k ohm source RF resistance to the diode 90k ohm RF resistance via RF impedance step-up transformation (maybe connecting the antenna to a tap on the tuned circuit, and leaving the diode on the top), good things happen.  (We will assume here that, in the impedance transformation to follow, the ratio of loaded-to-unloaded Q of the tuned circuits is not changed.)   For an impedance match, the tuned circuit resonant resistance should be transformed up by 9 times.  If this was done by a separate transformer (for ease of understanding) it would have a turns ratio of 1:3, stepping up the equivalent source voltage by 3 times and changing the equivalent source resistance to 90,000 Ohms.  What now?  Before matching, the diode got 9/10 of the source voltage applied to it.  Now it gets 1/2 the new equivalent source voltage (remember the equivalent voltage is 3 times the original source internal voltage).  The 1/2 comes from the 2:1 voltage division between the resistance of the equivalent source of 90,000 Ohms and the detector input resistance of 90,000 Ohms.  The ratio of the new detector voltage to the old  is: 3 times 1/2 divided by 0.9 = 1.67 times.  This equates to a 4.44 dB increase in power applied to the detector.  If the input signal to the detector is so weak that the detector is operating in the square-law region, the audio output power  will increase by 8.88 dB!  This is about a doubling of volume.

6A.   A Short tutorial on some aspects of audio transformer utilization in crystal sets. See Section 3 of Article 14 here

7.  Caution to observe when cutting the leads of a glass Agilent 5082-2835 Schottky diode (or any other glass diode):  When it is necessary to cut the leads of a glass packaged diode close to the glass body, use a tool that gives a scissors type of cut.  Diagonal cutters give a sudden physical shock to the diode that can damage its electrical performance.  This physical shock is greater than one might expect because of the use of plated steel instead of  more ductile copper wire. Steel is used, in part, because of its lower heat conductivity, to reduce the possibility of heat damage during soldering.

8.  Several different ways to look at a diode detector:

A diode detector can be thought of as a mixer, if one thinks of its input signal as consisting of two identical signals of equal power, in phase with each other.  It is well known that if a common AM mixer is fed with two signals of frequencies f1 and f2 Hz, most of the output it generates will consist of the second harmonic of each signal and two more signals at other frequencies.  One is at the sum frequency (f1+f2) Hz and one at the difference frequency (f1-f2).  Additional mixer products can be generated, but they will be weaker than those mentioned and will be neglected in this discussion.  In the case of an AM diode detector, we may consider that its input signal of power P Watts is in reality the sum of two equal in-phase signals, each of power P/2 and that there will be four output components, as stated above. They are:

9.  Using surface mount components in crystal radio sets:  A convenient way to connect to the tiny leads of small surface-mount diode and IC devices is to first solder them to a "Surfboard".  Pigtail leads can them be soldered through holes drilled in the Surfboard conducting races for connection to a circuit.

A surface mount device such as the OPA-349 integrated circuit (Eight lead SOIC package) can be soldered to a surfboard such as that manufactured by Capital Advanced Technologies: http://www.capitaladvanced.com .  Their Surfboards #9081 or #9082 are suitable and are available from various distributors such as Alltronics, Digi-Key, etc.

Surface mount diodes manufactured using the SOT-23 package can be handled using Surfboard #6103.  Diodes using the smaller SOT-323 package can be handled using Surfboard #330003.  This includes many Agilent surface mount diodes useful in crystal radio sets.  Packages containing multiple diodes exist that use the SOT-363 six lead package.  They can be handled using Surfboard #330006.  Agilent produces many of their Schottky diodes in dual, triple and quad form in the SOT-363 package.

It is recommended that anyone considering using Surfboards visit the above mentioned Website and read "Application Notes" and the "How-to Index".

10.  How to modify the tone quality delivered by headphones:  It is interesting to note that driving magnetic headphone elements with a high source resistance tends to improve the treble (making it sound brighter or tinny) and reduce the bass response, compared to the response when the AC source resistance matches the effective impedance of the elements.  Conversely, driving the headphone elements from a low resistance source tends to roll off the treble (making it sound dull) and relatively speaking, increase the bass.  With piezo ceramic or crystal elements, a high source resistance tends to reduce the treble and improve the bass response, compared to the response where the source resistance matches the effective impedance of the elements.  A low source resistance tends to reduce the bass and emphasize the treble.  Some piezo elements sound scratchy.  This condition can be minimized by driving the elements from a lower resistance source.

Here are some practical experimental ways to vary the audio source resistance of a crystal radio set when receiving weak-to-medium-strength signals.  A medium strength signal is defined as one at the crossover point between linear to square law operation (LSLCP).  See Figs. 2 & 3 in Article #15A. See the last paragraph of Article #17 for a way to determine if a diode detector is operating below or above its LSLCP.